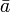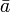A modo introductorio George Boole (1815 - 1864) fue un matemático y filósofo británico. Como inventor del álgebra de Boole, que marca los fundamentos de la aritmética computacional moderna, Boole es considerado como uno de los fundadores del campo de las Ciencias de la Computación. En 1854 publicó "An Investigation of the Laws of Thought" en el que desarrollaba un sistema de reglas que le permitían expresar, manipular y simplificar problemas lógicos y filosóficos cuyos argumentos admiten dos estados (verdadero o falso) por procedimientos matemáticos. Se podría decir que es el padre de las operaciones lógicas y gracias a su álgebra hoy en día es posible manipular operaciones lógicas.
Álgebra de Boole (también llamada Retículas booleanas) en informática y matemática, es una estructura algebraica que esquematiza las operaciones lógicas Y, O , NO y Si (AND,OR,NOT,IF), así como el conjunto de operaciones unión, intersección y complemento.
Hemos definido el conjunto A = {1,0} como el conjunto universal sobre el que se aplica el álgebra de Boole, sobre estos elementos se definen varias operaciones, veamos las más fundamentales:
Operación suma
| a | b | a + b |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 |
|
La operación suma (+) asigna a cada par de valores
a,
b de
A un valor
c de
A:
Su equivalencia en lógica de interruptores es un circuito de dos interruptores en paralelo.
Si uno de los valores de
a o
b es 1, el resultado será 1, es necesario que los dos sumandos sean 0, para que el resultado sea 0.
Operación producto
| a | b | a  b |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
La operación producto (
) asigna a cada par de valores
a,
b de
A un valor
c de
A:
Esta operación en lógica de interruptores es un circuito en serie de dos interruptores
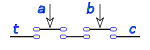
solo si los dos valores
a y
b son 1, el resultado será 1, si uno solo de ellos es 0 el resultado será 0.
Operación negación
| a |  |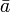
| 0 | 1 |
| 1 | 0 |
La operación negación presenta el opuesto del valor de
a:
Un interruptor inverso equivale a esta operación:
|
Operaciones combinadas |
Partiendo de estas tres operaciones elementales se pueden realizar
| a | b | |  |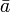
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 |
otras más complejas, que podemos representar como ecuaciones
booleanas, por ejemplo:
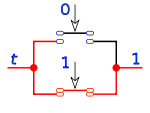
Que representado en lógica de interruptores es un circuito de dos interruptores en paralelo, siendo el primero de ellos inverso.
La distinta secuencia de valores de
a y
b da los resultados vistos en la tabla de verdad.
<><>
| |
|
Leyes fundamentales El resultado de aplicar cualquiera de las tres operaciones definidas a variables del sistema booleano resulta en otra variable del sistema, y este resultado es único.
1. Ley de idempotencia:
 
2. Ley de involución:
3. Ley conmutativa:
 
4. Ley asociativa:
 
5. Ley distributiva:
 
  
6. Ley de cancelación:
 
7. Ley de identidad:
 
 
8. Leyes de De Morgan:
 
|
|
|
|
<><>
García Zubia, Javier; Sanz Martínez, Jesús; Sotomayor Basilio, Borja. Universidad de Deusto. Departamento de Publicaciones. ed. Boole-Deusto v2.1 entorno de diseño lógico (2005 edición). ISBN 84-7485-973-5. Giménez Pradales, José Miguel. Universidad Politécnica de Cataluña. Departamento de Matemática Aplicada III. ed. Álgebra de Boole para ingeniera técnica (2004 edición). ISBN 84-933451-0-5. García Zubia, Javier; Sanz Martínez, Jesús; Sotomayor Basilio, Borja. Universidad de Deusto. Departamento de Publicaciones. ed. Boole-Deusto entorno de diseño lógico (2004 edición). ISBN 84-7485-929-8.
